Cálculos y Estimaciones

 

	This Project has been funded with support from the European Commission.  This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein.

 

Objetivos

Cuando finalice esta unidad podrá:

• Comprender el significado y los usos de los promedios y los promedios ponderados
• Resolver problemas relacionados

El promedio

Imaginemos que tenemos las calificaciones de un estudiante de instituto y estamos interesados en las notas de Matemáticas, Física, Informática, Química y Geografía.
Las notas van desde el 1 al 10, y para probar el conocimiento de las materias anteriores el estudiante tiene 4 evaluaciones.
Las notas se muestran en la siguiente tabla:

	Matemáticas	Física	Informática	Química	Geografía
1ª Evaluación	8	7	6	6	9
2ª Evaluación	9	9	8	8	10
3ª Evaluación	9	8	10	9	9
4ª Evaluación	10	8	10	8	10

Si queremos hacer el cálculo de su desempeño en Matemáticas, ¿Cómo lo haremos?, tenemos cuatro notas, y tenemos que combinarlas en un único valor. Si las sumamos, obtendremos un valor superior a 10 y eso no tiene sentido si no especificamos que el valor máximo es 40. Una manera de evitar esto es dividiendo la suma entre el número de notas, es decir, calcular el promedio:

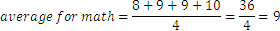
El valor obtenido está entre 1 y 10 y nos da una buena idea del rendimiento del estudiante en matemáticas.

Del mismo modo calculamos el promedio de Física:

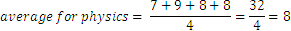
Hasta el momento, los valores obtenidos son enteros, pero no siempre es así:

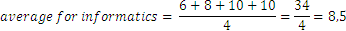
¿Qué es un número racional?
En general, la fórmula para el promedio, o media aritmética, es para dos números:

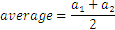
Para tres o cuatro números será:

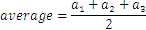
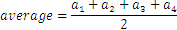
Para  números la fórmula es

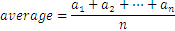
Es decir que sumamos todos los números y luego los dividimos por tantos cuantos números haya.
Para las otras dos asignaturas tenemos:

El promedio ponderado

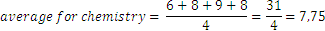
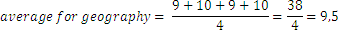
Imaginemos que ahora queremos obtener un tipo de puntuación para calcular las habilidades del estudiante en ciencias exactas, y pensamos que las matemáticas son ligeramente más importantes que la química o la física.
Por tanto, queremos asignar a la matemáticas una mayor importancia o ponderación y darle menor ponderación a la química. Asumiendo que la puntuación total es la unidad, imaginaremos que las notas en matemáticas tendrán el 50% de importancia, mientras que la informática tendrá el 30% y la física y la química tendrán un 10% de importancia cada una.
Repasemos los promedios de cada una:

Asignatura	Matemáticas	Física	Informática	Química
Promedio	9	8	8,5	7,75

La puntuación se calculará del siguiente modo:

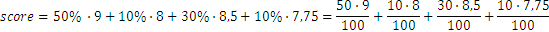
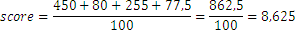
A la cantidad anterior la llamamos: el promedio ponderado, con una ponderación del 50%, 10%, 30% y 10% respectivamente. La suma de las ponderaciones da 100%. Otra manera de definir las ponderaciones es mediante los números fraccionarios que deben sumar todos 1, por ejemplo:  suman un total exacto de uno:

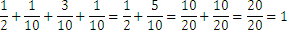
El correspondiente promedio ponderado se calcula de la siguiente manera:

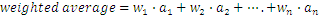
En general si tenemos  números nombrados como  y las correspondientes ponderaciones como , de tal modo que  ,su promedio ponderado será:

Como hemos visto anteriormente, las ponderaciones también pueden ser porcentajes ya que

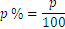
Vamos a calcular otro promedio ponderado para los números 130, 240, 100, 220 y 300 con ponderaciones  y . Vemos que:

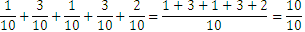
Y el promedio ponderado es:

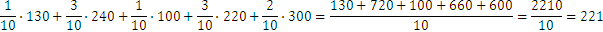
Deberíamos ver que el promedio (la media aritmética) definida anteriormente es un promedio ponderado en el que todas las ponderaciones son iguales a ..

 

 

Respuestas a las cuestiones y actividades planteadas en la Unidad Didáctica 6