Key Competencies Kit
for Facing Lifelong Learning


 |
Este proyecto ha sido financiado con el apoyo de la Comisión Europea. Esta comunicación refleja exclusivamente la opinión del autor; la Comisión no se hace responsable de uso alguno que pueda hacerse de la información aquí contenida |
 |
Una vez finalizado este modulo usted podrá:
A modo de recordatorio, hemos definido el conjunto de números enteros cómo
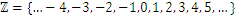
Para estos números hemos definido operaciones del tipo suma, resta, multiplicación y división. De ellas, la división es la única operación que no se puede efectuar entre cualquier número entero.
Cuando dividimos números enteros, podemos llegar a un punto donde el número a dividir por el segundo no da un resultado exacto, y en la división tenemos un resto.
Por ejemplo, si intentamos dividir 16 por 5 obtenemos un 3 y un resto de 1. Tenemos además la operación
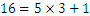
O en general
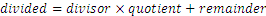
Imaginémonos que tenemos un segmento de longitud, y los dividimos en 3. Al poderse dividir 15 exactamente por 3, obtenemos tres segmentos de longitud 5. Pero ¿qué ocurre si dividimos un segmento de 16 cm entre 3 partes iguales? Es evidente que se puede hacer físicamente, pero ¿De qué longitud sería cada segmento?. Vamos a definir la longitud en el siguiente cálculo:
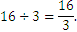
En general, para cualquiera de los enteros, definimos:
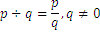
Donde  no puede ser 0. Estos números, que no sean enteros, son fracciones de los enteros, números fraccionarios, y se colocan en la línea numérica entre los números enteros tal y como se expresa a continuación:
no puede ser 0. Estos números, que no sean enteros, son fracciones de los enteros, números fraccionarios, y se colocan en la línea numérica entre los números enteros tal y como se expresa a continuación:
-3 -2 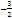 -1 0 1 2
-1 0 1 2 ![]() 3
3
Observe que  está entre
está entre 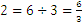 and
and 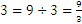 .
.
Tenga en cuenta que el número entero 2 se puede representar cómo un número fraccionario de más de una manera: 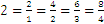 y lo mismo se aplica a cualquier número fraccionario.
y lo mismo se aplica a cualquier número fraccionario.
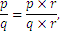
Para cada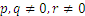 entero.
entero.
Para cualquier número fraccionario  ,
, 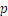 is called the numerator and
is called the numerator and 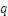 es el numerador y
es el numerador y  es el denominador. Dos fracciones se pueden escribir como si tuvieran el mismo denominador, multiplicando cada numerador y denominador de la fracción por el denominador de la otra fracción:
es el denominador. Dos fracciones se pueden escribir como si tuvieran el mismo denominador, multiplicando cada numerador y denominador de la fracción por el denominador de la otra fracción:
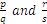 se puede escribir como
se puede escribir como 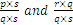 .
.
De este modo podemos determinar el número mayor como la fracción con el numerador mayor cuando escribamos las fracciones con el mismo denominador. Por ejemplo, comparemos los números  y
y  :
:
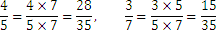
Al ser 15 menor que 28, obtenemos que  es mayor que
es mayor que  .
.
El conjunto de todos los números fraccionarios se denomina con  y contiene todos los enteros, y todos los fraccionarios obtenidos al dividir dos enteros. En este conjunto se define la suma del siguiente modo:
y contiene todos los enteros, y todos los fraccionarios obtenidos al dividir dos enteros. En este conjunto se define la suma del siguiente modo:
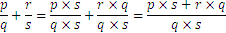
Por ejemplo:
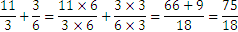
La resta se define de una manera análoga
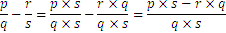
La multiplicación sigue el siguiente patrón
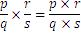
Como en el siguiente ejemplo
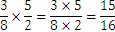
La división tiene una forma distinta, ya que se reemplaza con la multiplicación de la primera fracción con la segunda fracción invertida:
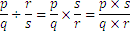
El siguiente ejemplo lo ilustra:
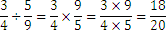
Cómo hemos observado anteriormente, cualquier número racional se puede representar de más de una manera. Sin embargo, existe una forma que es única para cada número racional. Presentamos los números racionales cuando el resultado de una división que nos exacta debido al resto, a continuación veremos lo que pasa si continuamos la división después de obtener un resto:Después de obtener 3 que es menor que 15, añadimos 0 a la izquierda y continuamos la división, y en el cociente los dígitos resultantes deberían estar precedidos de una coma.
Vemos que 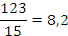 , que es un número fraccionario entre 8 y 9. Esta es la representación decimal de un número racional. La parte situada a la derecha de la coma representa que parte del dividendo es resto de la división del entero. Podemos dibujar esta parte decimal como una fracción del total. Si dividimos 1 por 2, obtenemos 0,5 que representa la mitad de 1, y que se corresponde con la división de un segmento de longitud uno en dos partes iguales. Lo mismo se puede decir del resultado de dividir 1 por 4, que es 0,25 y que es un cuarto del un segmento con longitud uno.
, que es un número fraccionario entre 8 y 9. Esta es la representación decimal de un número racional. La parte situada a la derecha de la coma representa que parte del dividendo es resto de la división del entero. Podemos dibujar esta parte decimal como una fracción del total. Si dividimos 1 por 2, obtenemos 0,5 que representa la mitad de 1, y que se corresponde con la división de un segmento de longitud uno en dos partes iguales. Lo mismo se puede decir del resultado de dividir 1 por 4, que es 0,25 y que es un cuarto del un segmento con longitud uno.
0,25 0,5 0,75 1

Podemos realizar sumas con los números racionales cuando tienen representación decimal. Serían como en el caso de los números enteros excepto porque tenemos que hacer coincidir las comas y completaremos el número más corto con ceros. Por ejemplo, si queremos sumar 12,35 y 1,6:
| 1 | 2 |
, |
3 |
5 |
|
1 |
, |
6 |
0 |
1 |
3 |
, |
9 |
5 |
La misma regla se aplica a la resta. En el caso de la multiplicación, hacemos multiplicaciones sin tener en cuenta las comas, y luego ponemos la coma en la posición a+b desde la derecha. En este caso a es el número de dígitos después de la coma del primer número y b es el número de dígitos después de la coma (los decimales) del segundo número.
En el caso de los números anteriores, 12,35 y 1,6 observamos que el primero tiene 2 decimales mientras que el segundo tiene sólo uno, por tanto el resultado tendrá 3 decimales, es decir dígitos después de la coma.
|
1 |
2 |
3 |
5 |
|
|
|
1 |
6 |
|
7 |
4 |
1 |
0 |
1 |
2 |
3 |
5 |
|
1 |
9 |
7 |
6 |
0 |
Multiplicamos los números naturales 1.235 y 16 y obtenemos 19.760. El resultado final en este caso es 19,760 o 19,76, ya que los ceros a la derecha no representan ninguna diferencia en la representación de los números fraccionarios.
En el caso de la división, ampliamos los dígitos a la derecha como en la suma y eliminamos las comas.
Un caso especial de las fracciones son los porcentajes que se utilizan para representar cuánto supone una parte que está contenida dentro de una unidad. Por ejemplo nos gustaría saber qué cantidad supone 18 respecto a un total de 90. Para poder averiguarlo, tenemos que dividir 18 por 90 y obtener 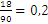 que es lo mismo que
que es lo mismo que 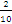 o
o 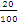 o 20 de 100 o 20por ciento.
o 20 de 100 o 20por ciento.
The usual notation is 20%. It is obvious that any number taken out of 100 represents that number % of 100: 33 represents 33% of 100.
La anotación normal es 20%. Es evidente que cualquier número que que se toma respecto a 100 representa el % de 100: 33 representa 33% de 100.
Los cálculos se pueden hacer de otro modo, siempre podemos determinar qué exactitud tiene el p% de un número: 120% de 35 es
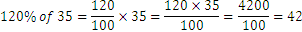
En general
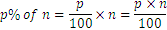
En cambio, la determinación de un porcentaje es
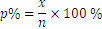
Aplicación
Vamos a resolver un problema que lleva porcentajes. Asumamos que hacemos un depósito de 8.000€ en el banco, con un interés al 6% anual. ¿Cuánto habrá en la cuenta al finalizar el año? ¿Y pasados tres años?
Llamemos S al importe inicial de dinero, por ejemplo, tenemos
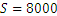
Pasado un año, el interés es 6% del importe inicial, es decir:
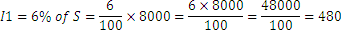
La cantidad final pasado un año sería:
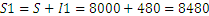
Para el segundo año, el interés sería
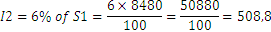
Por tanto
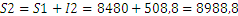
Finalmente
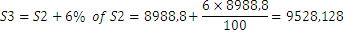
Otro modo de resolver el problema es viendo que cada año tenemos el importe inicial más un 6% es decir:
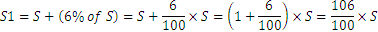
El primero significa que pasado un año tenemos 106% del importe inicial. Por tanto pasados tres años obtenemos lo siguiente:
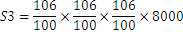

 |
Respuestas a las cuestiones y actividades planteadas en la Unidad Didáctica 2 |
Pregunta 1:
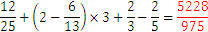
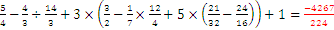
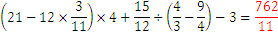
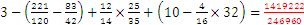
Pregunta 2:
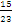 or
or 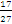 ,
, 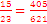 is greater than
is greater than 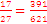
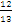 or
or 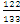 ,
, 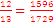 is greater than
is greater than 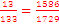
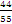 or
or  , the numbers are equal
, the numbers are equal 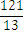 or
or 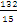 ,
, 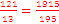 is greater than
is greater than 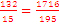
Pregunta 3:
The representation order is 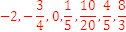 , the smallest is -2 and the largest is 8/3.
, the smallest is -2 and the largest is 8/3.
Pregunta 4:
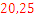
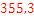
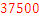
Pregunta 5:
A person makes a deposit of 1000 RON with an interest of 10% per year. After one year the sum will be 1100 RON. About after 5 years he will have 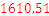 RON.
RON.