Calculation and Estimation

 

	This Project has been funded with support from the European Commission.  This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein.

 

Objectives

Upon completion of this unit you shall be able to:

• Understand the meaning and uses of averages and weighted averages
• Solve related problems

 

The average

Let’s assume we have the school record of a high school student, and we are interested in the grades obtained in Mathematics, Physics, Informatics, Chemistry and Geography.
The grades range from 1 to 10, and for each of the above domains the student has 4 evaluations.
The grades are given in the following table:

	Mathematics	Physics	Informatics	Chemistry	Geography
1st Grade	8	7	6	6	9
2nd Grade	9	9	8	8	10
3rd Grade	9	8	10	9	9
4th Grade	10	8	10	8	10

Let’s say we are interested in evaluating the activity in Mathematics, but how do we do it? We have 4 grades, and we have to combine them in one single value. If we sum them up we get a value larger than 10, and it’s not very relevant if don’t specify that the maximum value is 40. A way to avoid that is to divide the sum by the total number of grades, that is, to do an average:

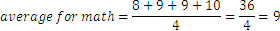
The value obtained is between 1 and 10 and gives us a good idea of the student performances in mathematics.

The same way we will evaluate the average for physics:

So far the values obtained are integers, but that is not always the case:

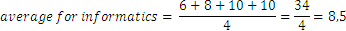
which is a rational number.
In general, the formula for average, or arithmetic mean, is given for two numbers by:

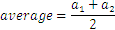
For three and four numbers we have:

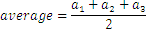
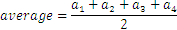
For  numbers the formula is

Namely, we add all the numbers, and then we divide by how many they are.

For the remaining two disciplines we have:

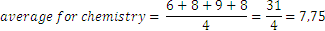
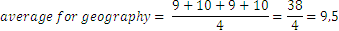
THE WEIGHTED AVERAGE

Let’s assume now that we want to compute some kind of score in order to evaluate the student’s abilities in exact sciences, but we feel that mathematics is slightly more important than chemistry, or physics.
Therefore we will want to assign a greater importance or weight to mathematics and a smaller weight to chemistry. Assuming the whole score is a unit, we will imagine that the grades in mathematics will have 50% importance, while informatics will have 30% and physics and chemistry will have each 10% importance.
We recall the averages for each:

Domain	Mathematics	Physics	Informatics	Chemistry
Average	9	8	8,5	7,75

The score will be evaluated in the following manner:

We call the above quantity: the weighted average, with the weights 50%, 10%, 30% and 10% respectively. The weights add up to 100%. Another way of defining the weights is by means of fractional numbers, all adding up to 1, for instance:  added amount to exactly one:

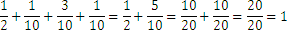
The corresponding weighted average is computed in the following manner:

In general, if we have  numbers denoted by  and the corresponding weights  denoted by , such that  their weighted average is given by:

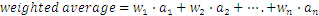
As we have seen above, the weights can also be percents, since

Let’s compute another weighted average, for the numbers 130, 240, 100, 220 and 300 with weights  and . We notice that

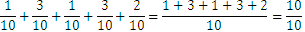
and the weighted average is

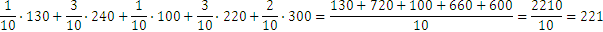
We should notice that the average (arithmetic mean) defined before is an weighted average with all weights equal to .