Key Competencies Kit
for Facing Lifelong Learning


 |
This Project has been funded with support from the European Commission. This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein. |
 |
Una vez completada esta unidad usted podrá:
Recordemos que todos los números definidos hasta ahora, los llamados enteros, y los números fraccionarios se pueden representar en una línea de puntos. Pero no todos los puntos de una línea pueden representarse con números fraccionarios. Estos números junto con los números fraccionarios se denominan los números reales, y su conjunto se denomina con 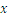 . Cualquier número real que no se pueda representar como un número fraccionario se puede considerar como un número fraccionario con un número ilimitado de dígitos a la derecha de la coma.
. Cualquier número real que no se pueda representar como un número fraccionario se puede considerar como un número fraccionario con un número ilimitado de dígitos a la derecha de la coma.
Otro número es “el número que al multiplicarlo por sí mismo es igual a 2” también llamada la raíz cuadrada de 2, pero veremos las raíces cuadradas al detalle más adelante.
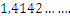 un número real que al multiplicarlo por si mismo es 2.
un número real que al multiplicarlo por si mismo es 2.
Todas las operaciones del tipo suma, resta, multiplicación y división se realizan con todos los números reales. Los números reales tienen las mismas propiedades y siguen el mismo orden de operaciones. En la práctica, nunca trabajaremos con números reales que no tengan fracciones ya que se trataría de números que tendrían un número ilimitado de decimales y por tanto no podríamos trabajar con todos los dígitos, así que sólo usaremos unos pocos.
Resumamos las propiedades de las cuatro operaciones:
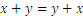
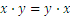
(hemos utilizado “ ” en lugar de “
” en lugar de “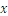 ” para la multiplicación )
” para la multiplicación )
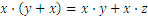

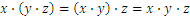
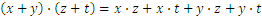
En el tema anterior, nos hemos encontrado con las siguientes operaciones:
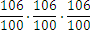
Una mejor manera de escribir las multiplicaciones repetidas de un número por sí mismo, es utilizar las potencias. Por ejemplo, podemos escribir el resultado de  como
como 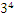 que significa que 3 se multiplica por si mismo 4 veces. El resultado es 81.
que significa que 3 se multiplica por si mismo 4 veces. El resultado es 81.
En general
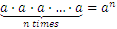
Y el resultado se lee como“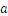 a la
a la 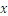 potencia”. En el caso de los números enteros, los cálculos son fáciles, pero para los números fraccionarios, hay una serie de reglas adicionales, del tipo:
potencia”. En el caso de los números enteros, los cálculos son fáciles, pero para los números fraccionarios, hay una serie de reglas adicionales, del tipo:
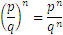
Las más importantes son las potencias al cuadrado (2) y al cubo (3). El número 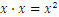 se lee como “
se lee como “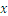 al cuadrado”. Hay que tener en cuenta que el cuadrado de cualquier número natural es un número natural como en el caso de todos los números racionales. Pero ¿Podemos definir una correspondencia inversa entre un número y el número que es su cuadrado? Por ejemplo, para 4, el número que da 4 cuando se eleva al cuadrado es 2:
al cuadrado”. Hay que tener en cuenta que el cuadrado de cualquier número natural es un número natural como en el caso de todos los números racionales. Pero ¿Podemos definir una correspondencia inversa entre un número y el número que es su cuadrado? Por ejemplo, para 4, el número que da 4 cuando se eleva al cuadrado es 2:
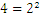
Lo mismo pasa con el 9 y el 3, 16 y 4, y así sucesivamente. Denominaremos a dicho número como “la raíz cuadrada de”, por tanto, la raíz cuadrada de 9 es 3, y la raíz cuadrada de 16 es 4. También escribiremos

En general tenemos:
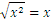
Para cada x mayor de 0.
Estos son algunas fórmulas útiles para trabajar con números reales:
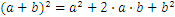
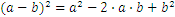
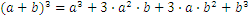
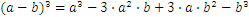

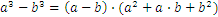
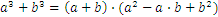
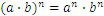
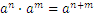
Vamos a asumir que tenemos el siguiente problema: nos movemos de la ciudad A a la ciudad B, a una velocidad de 60km por hora, y la distancia entre las dos ciudades es de 30km. ¿Cuánto nos llevará llegar a la ciudad B?
Primero escribimos

donde 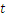 es el tiempo necesario. Sabemos que multiplicando la velocidad por el tiempo, obtenemos la distancia así que reemplazamos el tiempo por 60 y la distancia por 30. Para obtener el valor de
es el tiempo necesario. Sabemos que multiplicando la velocidad por el tiempo, obtenemos la distancia así que reemplazamos el tiempo por 60 y la distancia por 30. Para obtener el valor de  debemos dividir por 60 ambos lados de la ecuación (la igualdad) anterior.
debemos dividir por 60 ambos lados de la ecuación (la igualdad) anterior.
Obtenemos:
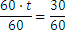
Y
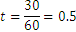
Por tanto 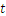 es media hora.
es media hora.
En general, trabajamos con ecuaciones del tipo.
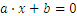
Los pasos para resolver la ecuación anterior cuando se conoce el valor de 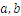 son los siguientes:
son los siguientes:
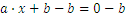
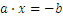
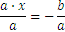
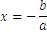
Otro formato de ecuación es:
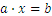
Como el que resolvimos en el ejemplo anterior.
Resolvamos el siguiente ejemplo
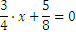
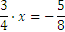

Otro ejemplo de su aplicación es el siguiente: asumamos que una persona tiene una cuenta bancaria con 2.500 € y se desconoce el tipo de interés. Pasado un año, la cuenta tiene 2.650 €. Queremos saber el tipo de interés, asumiendo que ha sido el mismo durante todo el año. Tenemos la siguiente ecuación.
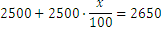
Tenemos después de mover 2.500 a la derecha
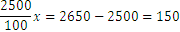
Por tanto:
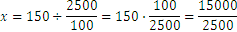
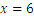
Así que el tipo de interés es 6% anual.
Veamos el siguiente problema: John y Jane son hermanos. Hacer diez años, John tenía el doble de edad que Jane y dentro de cinco años será 5 años más viejo que ella. ¿Cuántos años tienen ahora?. Para resolver este problema denominamos x e y la edad de John and Jane, respectivamente. Tenemos:
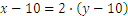
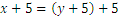
Trabajaremos con la segunda ecuación, para poder obtener una igualdad de x que contenga y. Es decir
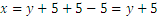
Substituimos x en la primera ecuación por esta igualdad
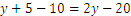
Y luego movemos todas las y a la derecha, y el resto a la izquierda
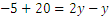
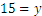
Ya que 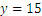 y
y  por tanto
por tanto  .
.
Recordemos el problema que teníamos anteriormente, con el depósito inicial de 2.500 y un interés desconocido. Supongamos que sólo sabemos que la suma de dinero pasados 2 años es de 2.809. En este caso, tenemos
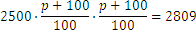
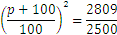
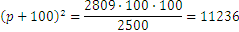
Podemos hacer la raíz cuadrada de ambas partes y obtener

y 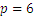 .
.

 |
Respuestas a las cuestiones y actividades planteadas en la Unidad Didáctica 3 |
Pregunta 1:
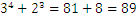
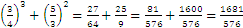
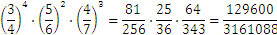
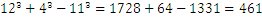
Pregunta 2:

Pregunta 3:
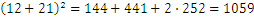


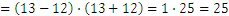

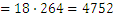
Pregunta 4:

Pregunta 5: