Real numbers

 

	This Project has been funded with support from the European Commission.  This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein.

Objectives

Upon completion of this unit you shall be able to:

• Effectuate basic operations with floating point numbers
• Representation and find relationships between real numbers.       
• Solve simple linear equations           
• Solve other applications

 

Introduction and representation

Let us recall that all numbers define so far, namely the integers and the fractional numbers can be represented on a line as points. But not all the points on a line can be represented by fractional numbers. These numbers along with the fractional numbers are called the real numbers, and their set is denote by . Any real number that may not be represented as a fractional number can be thought as a fractional number with an unlimited numbers of digits to the right of the comma.
One such number is “the number which, multiplied by itself, equals 2” also called the  square root of 2, but more on the square root of a number a little bit later.

 is a real number, which multiplied by itself is 2

All operations such as addition, subtraction, multiplication and division can be extended to all real numbers.  Same properties and the order of operations are true for the real numbers. In practice, we will almost never work with numbers that are not fractional, since real numbers that are not fractions have infinite number of decimals, therefore we cannot work with all of the digits, so we will use only a number of them.

Let us summarize the properties of the four operations:

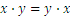
(we have used the notation “” instead of “” for multiplication )

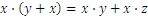
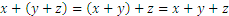
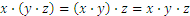
In a previous lesson we have encountered the following operations:

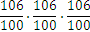
A better way to write repeated multiplications of a number by itself is to use the power notation. For instance the result of 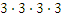 could be written as  meaning that 3 is multiplied with itself 4 times. The result is 81.

In general

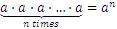
And the result is read as “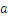 to the th”. For integer numbers the calculations are easy, but for fractional numbers there are some additional rules, such as:

The most important cases are when the power is two or three. The number 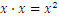 is read as “ squared”. One observation is that the square of any natural number is still a natural number, as is the case for all rational numbers. But can we find an inverse correspondence, between a number and the number who’s square it is? For instance, for 4, the number that equals 4 when squared is 2:

Same is true for 9 and 3, 16 and 4, and so on.  We will denote such a number by “ the square root of”, therefore the square root of 9 is 3, and the square root of 16 is 4. We also write

In general we have

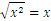
for any  greater than 0.

Here are some additional useful formulae for working with real numbers:

Linear equations

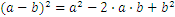
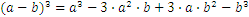
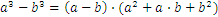
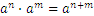
Let us assume that we have the following problem: we are moving from the city A to the city B, at a speed of 60km per hour, and the distance between the two cities is 30km. How long will it take to get there?

We solve this by writing first of all

where 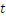 is the necessary time. We know that multiplying the speed with the time we get the distance, so we replaced the speed with 60 and the distance with 30. In order to obtain the value of  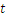we must divide by 60 on both parts of the equality above, also called equation. We get

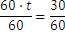
Further we get

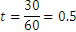
That is 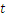 is a half of an hour.

In general, we are dealing with equations of the following form

The general steps for solving the above equation, when 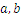 are known are the following:

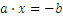
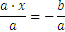
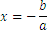
Another form for an equation is

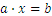
as the one we solved in the example above.
Let us solve another example

Another example of application is the following: let’s assume a person has a bank account amounting 2500 RON and the interest rate is unknown. After one year the account holds 2650 RON. We want to find the interest rate, assuming it has stayed the same over the year. We have the following equation

We have, after moving 2500 to the right side

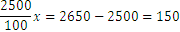
therefore

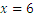
So the interest rate is 6% per year.

Applications

Let’s take a look at the following problem: John and Jane are brothers. Ten years ago, John had twice of Jane’s age, and in five years he will be 5 years older than her. How old are they now? In order to solve this problem we denote by 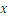 and 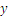 the age of John and Jane, respectively. We have

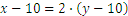
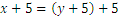
We shall work on the second equation, in order to obtain  as an expression containing. We get

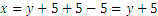
We use this expression for 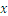 and substitute it in the first equation

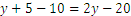
And then we move all the terms containing 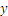 to the right, and the rest to the left

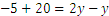
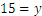
Since  and  as we have seen before, we get .

Let us recall the problem we had earlier, with the initial deposit of 2500 and unknown interest rate. Let’s suppose that we only know the sum of money after 2 years, and it is 2809. In this case we have

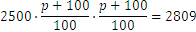
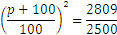
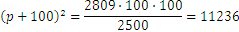
Now we can take the square root of both members and obtain

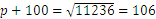
and 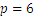.