Key Competencies Kit
for Facing Lifelong Learning


 |
This Project has been funded with support from the European Commission. This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein. |
 |
Upon completion of this unit you shall be able to:
Let us recall that, so far, we have defined the set of integers as
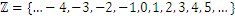
For these numbers we have defined operations such as addition, subtraction, multiplication and subtraction. Out of all these four operations, division is the only operation that cannot be effectuated between any integer numbers.
When dividing integers we can get to a point where the number divided is not exactly dividable by the second, and in the division algorithm we get a remainder.
For instance, if we try to divide 16 by 5 we get 3 and a remainder of 1. We have thus the representation

or, in general
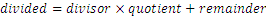
Let us now imagine that we have a segment of length 15, and we divide it in three. Since 15 can be divided exactly by 3, we get three segments of length 5. But what happens if we divide a 16 cm segment in 3 equally long pieces? Clearly it can be done physically, but what about the length of that segment? We define that length by the notation:
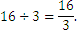
In general, for any two integers, we define
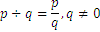
where ![]() cannot be 0. These numbers, which are not integers, are fractions of integers, or fractional numbers, and they are positioned on the line between the integer numbers, as in the figure below:
cannot be 0. These numbers, which are not integers, are fractions of integers, or fractional numbers, and they are positioned on the line between the integer numbers, as in the figure below:
-3 -2  -1 0 1 2
-1 0 1 2  3
3
Let us notice that  is between
is between
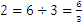 and
and 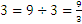 .
.
We also note that the integer number 2 can be represented as a fractional number in more than one way: 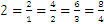 and the same is true for any fractional number.
and the same is true for any fractional number.
In general
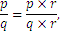
for any 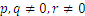 integers.
integers.
For any fractional number  ,
, 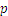 is called the numerator and
is called the numerator and 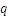 is called the denominator. Any two fractions can be written as to have the same denominator, by multiplying each fraction’s numerator and denominator with the denominator of the other fraction:
is called the denominator. Any two fractions can be written as to have the same denominator, by multiplying each fraction’s numerator and denominator with the denominator of the other fraction:
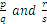 can be written as
can be written as 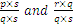 .
.
This way we can define the larger number as the fraction with the largest numerator when we write the fractions as to have the same denominator. For instance let us compare the numbers  and
and  :
:
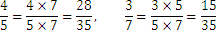
Since 15 is smaller than 28, we get that  is greater than
is greater than  .
.
The set of all fractional numbers is denoted by 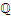 and contains all integers, and all fractions obtained by dividing any two integers. We define addition on this set in the following manner:
and contains all integers, and all fractions obtained by dividing any two integers. We define addition on this set in the following manner:
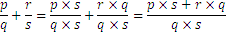
For instance
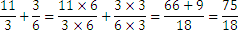
Subtraction is defined in an analogue manner
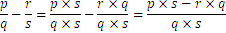
Multiplications follow the pattern below
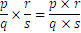
as in the next example
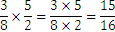
Division takes a slightly different form, as it is replaced with the multiplication of the first fraction with the reversed second fraction:

The example below illustrates that:
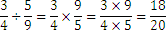
We noticed earlier that any rational number may be represented in more than one form. However, there is one form that is unique for each rational number. We introduced the rational numbers as the result of divisions that cannot be completed, because of the remainder. In the following we shall see what happens if we continue the division after we reach the remainder:
 123 15
123 15
![]() 120 8,2
120 8,2
= 30
 30
30
=
After we obtain 3, which is smaller than 15, we add a zero to the left, and continue the division, the following digits in the result being preceded by a coma.
We get that 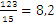 , which is a fractional number between 8 and 9. This representation is the decimal representation of a rational number. The part situated on the right of the dot represents how much of the divider is the remainder of the integer division. We can picture this decimal part as a fraction of a whole. If we divide 1 by 2, we get 0,5 which represents one half of 1, corresponding to the division of a segment of length one in two equal parts. The same can be said about the result of dividing 1 by 4, which is 0,25, that is a quarter of a segment of length one.
, which is a fractional number between 8 and 9. This representation is the decimal representation of a rational number. The part situated on the right of the dot represents how much of the divider is the remainder of the integer division. We can picture this decimal part as a fraction of a whole. If we divide 1 by 2, we get 0,5 which represents one half of 1, corresponding to the division of a segment of length one in two equal parts. The same can be said about the result of dividing 1 by 4, which is 0,25, that is a quarter of a segment of length one.
0,25 0,5 0,75 1

We can perform additions with rational numbers in the decimal representation, just as if we were adding integers, except that we must align the corresponding commas, and we must complete the shorter number with trailing zeros, as in the following example, where we add 12,35 and 1,6:
| 1 | 2 |
, |
3 |
5 |
|
1 |
, |
6 |
0 |
1 |
3 |
, |
9 |
5 |
Same rule applies for subtraction. In the case of multiplication we make the multiplication regardless of commas, and then we position the comma at a+b positions from right, where a is the number of digits after the comma for the first number, and b is the number of digits after the comma (decimals) for the second number.
For the numbers above, 12,35 and 1,6 we notice that the first has 2 decimals, while the second only has one, therefore the result will have 3 decimals, that is digits after the coma.
|
1 |
2 |
3 |
5 |
|
|
|
1 |
6 |
|
7 |
4 |
1 |
0 |
1 |
2 |
3 |
5 |
|
1 |
9 |
7 |
6 |
0 |
We multiply the natural numbers 1235 and 16 to get 19760. The final result will be 19,760 or 19,76, as the rightmost zeroes make no difference to the decimal representation of a fractional number.
For division we extend the digits to the right like for addition, and we eliminate the commas.
A special case of fractions are percents, which are used to represent how much a part accounts for in an containing unit. For instance we would like to know how much is a quantity of 18 from a total of 90. In order to find that out we divide 18 by 90 to get 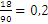 which is the same as
which is the same as 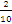 or
or 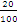 or 20 out of 100 or 20 percent.
or 20 out of 100 or 20 percent.
The usual notation is 20%. It is obvious that any number taken out of 100 represents that number % of 100: 33 represents 33% of 100.
The calculations can go the other way too, we can always determine how much exactly is p% of a number: 120% of 35 is
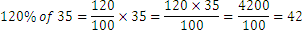
In general
![]()
Conversely, the determination of the percent follows
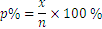
Application
Let’s solve a problem involving percents. Let us assume that we make a deposit of 8000 RON to the bank, at an interest rate of 6% per year. How much does the account holds after one year? How about 3 years later?
Let us denote by S the initial sum of money, i.e. we have
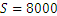
After one year, the interest is 6% of the initial sum, that is:
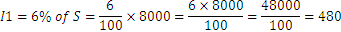
The sum after one year will be
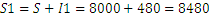
For the second year, the interest will be
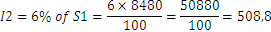
Therefore
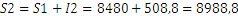
Lastly
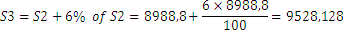
Another way of solving the problem is to notice that after each year we have the initial sum plus 6% that is:
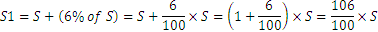
The former means that after one year we have 106% of the initial sum. After three years we will obtain the following: