Дробни числа: Основни операции с дробни числа

 

	Този проект е финансиран с помощта на Европейската комисия. Този документ отразява гледната точка единствено на автора и Комисията не може да бъде отговорна за употребата на информацията в него.

 

Цели:

След успешно приключване на модула обучаемият ще може да:

• Разбирате използването на дробните числа
• Привеждате в изпълнение дробните числа
• Можете да използвате проценти и съотношения
• Прилагате дробните числа в реални ситуации

Въведение

Нека си припомним, че досега, ние имаме определени набор от цели числа, като

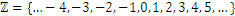
За тези числа вече обсъдихме определени операции като събиране, изваждане, умножение и делене. От всички тези четири операции, деленето е единствената дейност, която не може да бъде извършена между всички естествени числа.
При делене числата могат да стигнат до точката, където броят разделени не е точно равен на тези от друга страна, и в делителния алгоритъм получаваме остатъка.
Например, ако искаме да разделим 16 на 5, то можем да го изобразим като 3 плюс 1. Можем и да отбележим, че ако търсим абсолютното делимо то тогава то ще бъде равно на 3,2.

Като правило
Частното = делимото по делителя

Ето още един пример при които можем да изобразим процеса делене. Това може да стане като използваме дроб, в която над дробната черта е числителят, а под нея знаменателят.

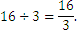
Можем да използваме правилото, че всяко цяло число може да бъде разделено на друго цяло число, което да е различно от 0.

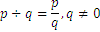
Тези цифри, които не са цели числа, са части от цели числа, числа или частични, а те са разположени на границата между цели числа, като на фигурата по-долу::

      -3       -2 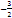     -1       0       1        2        3

Например    се намира между  и .
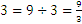Например числото  2 може да бъде представено по няколко начина чрез дробно число както следва: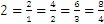  

Правило:

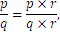
за всяко .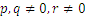

При всяка дроб   , 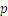се нарича числител, а всяко  е знаменател. Числителят и знаменателят също могат да бъдат изобразявани като допълнителна операция на умножение. Например:

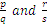 se puede escribir como .

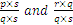 може да бъде  .

По този начин ние можем да определим по-голям брой като част с най-голям числител, когато се пише на фракции, че да имат едни и същи знаменател.
Нека да сравним   и  :

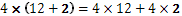
Тъй като 15 е по-малко от 28, може да заключим, че   е по-голямо от  .

  

Основни операции

Съвкупността от всички дробни числа се означава с 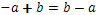 и съдържа всички числа, както и всички фракции, получени чрез разделяне всеки две цели числа. Ние дефинираме този набор по следния начин:

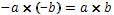
Ето още един пример при събиране:

Изваждането се осъществява по аналогичен начин:

Умножението става по този модел:

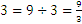
Разделянето влиза в една малко по-различна форма, тъй като тя се заменя с умножаването в първата част с обърнати числител и знаменател:

Ето и реален пример за това:

Десетична точка

Забелязахме, по-рано, че всяко рационално число може да бъде представено в повече от една форма. Все пак има форма, която е уникална за всеки рационално число. Видяхме, че при делението на някой числа не можем да получим точно цяло число и оставя винаги едно на ум. В следващата схема ще видим какво се случва ако продължим разделянето докрай, без да имаме едно на ум.

След като получихме числото 3, което е по малко от 15, ние добавихме една 0 (вижте в лявата колона) и продължаваме с делението, като резултата ще бъде представен със десетична точка.  
По този начин се получи, че   , което представлява десетична дроб между 8 и 9.
Този начин на представяне като знак след десетичната точка практически представя рационално число. Частта, разположен след десетичната точка показва колко голяма част от разделителя е остатъка от целочислено делене.

Ако разделим 1 на 2, получава 0,5, което представлява половината от един, което съответства на разпределението на даден сегмент от една дължина на две равни части.
По същия начин ако разделим 1 на 4 ще получим 0,25. Нарича се четвърт от сегмента на единица.

 

0,25                 0,5                   0,75                    1
 

Ние може да работим с рационални числа в десетичен представяне, като например ако бяхме добавили числа, освен че трябва да се съобразят въпросните запетайки, и ние трябва да попълнят кратък номер с остатъчна нули, като в следния пример, когато ние добавяме 12 ,35 и 1,6:

Същото правило може да приложим и при изваждане. В случай на умножение ние може да получим и повече цифри след десетичната точка. 
Например при 12,35 имаме десетична точка след втората цифра, а при 1,6 след първата.

Проценти

Специфичен случай на дроби представлява смятането чрез проценти. Например ако искаме да знаем колко е точно разликата от 18 делено на 90, то ще получим 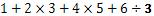 , което представлява същото съотношение както е  или  , което представлява 20 от абсолютното 100 или с други думи казано 20 процента.

Да не забравяме, че всяко цяло число съотнесено процентно към 100 представлява и неговия процент. Например 33 към 100 представлява 33% от 100.
Как обаче ще изглежда ако искаме да видим колко прави 120 % от 35. Вижте внимателно следващия пример.

Прилагане на практика

Нека да използваме сега знанията на практика. Да предположим, че искаме да внесем в банка депозит от 8000 ЛЕВА при лихва 6% на година. С колко ще се увеличат внесените пари след една година? А след 3?
Нека обозначим с  S първоначалната сума пари, тоест имаме
, а със знак l1 ще отбележим времето – тоест една година.
След една година при 6% лихва ще получим следното:

Това означава, че след една година ще получим към депозита си 480 ЛЕВА.

За втората година – 508, 80 ЛЕВА

Тоест в края на втората година нашата банкова сметка ще бъде 8988, 80 ЛЕВА.

А нека сега видим за третата година – сумата ще нарастне на 9528,128 ЛЕВА.

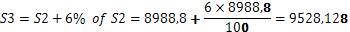
Друг начин за да намерите крайния резултат е следната операция показана по долу. S1 обозначава първата година.

Формално казано това означава, че след една година ще имаме 106% от първоначално внесената сума. За да намерим след три години трябва да извършим следното пресмятане, като с S3 отбелязваме третата година: