Key Competencies Kit
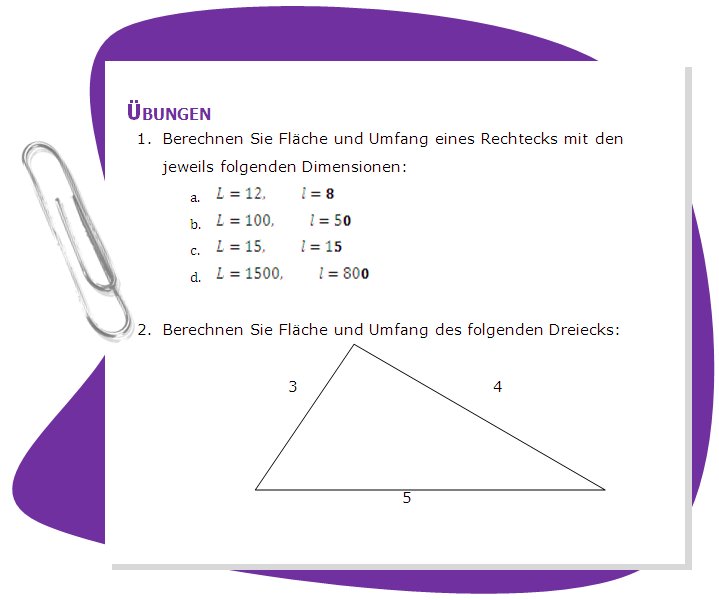
for Facing Lifelong Learning
 |
Este proyecto ha sido financiado con el apoyo de la Comisión Europea. Esta comunicación refleja exclusivamente la opinión del autor; la Comisión no se hace responsable de uso alguno que pueda hacerse de la información aquí contenida |
 |
Nach Abschluss dieser Lehreinheit sollten Sie:
In der Natur finden wir viele Objekte unterschiedlicher Form. Ihre Grundformen werden geometrische Figuren genannt.
Die einfachste geometrische Figur ist das Segment. Wir können ein Segment einfach als eine Gerade zwischen zwei Punkten zeichnen.
Ein Segment:
Die wichtigste Eigenschaft eines Segments ist seine Länge. Da jede Entfernung zwischen zwei Objekten ein Segment darstellt, benötigen wir eine Methode, um die Entfernung zu beschreiben. Wir verwenden ein Lineal, ein gerades Stück Holz, auf welchem sich in gleichen Abständen Längenmarkierungen befinden.
Als nächstes wollen wir nun über die Figur des Segments hinausgehen. Eine der wichtigsten geometrischen Figuren ist das Rechteck: :
In unserer Umgebung sehen wir eine Menge solcher Objekte – eine Zeitung, ein Stück Papier, ein landwirtschaftliches Feld, eine Wand und so weiter.
Nehmen wir an, wir müssten für ein Grundstück einen Zaun konstruieren und herausfinden wie viele Planken für den Zaun benötigt werden.
Die Gesamtlänge des Zaunes erhalten wir bei diesem (rechteckigen) Grundstück durch Aufsummieren der Seitenlängen. Wenn die Seiten AB, BC, CD und AD sind, ergibt sich der Umfang aus
Bei einem Rechteck sind die gegenüberliegenden Seiten immer gleich lang. Wir können also die die längere Seite mit 
und die kürzere mit 
bezeichnen und damit das Rechteck genau beschreiben. Der Umfang des Rechtecks ergibt sich dann mit
Eine weitere interessante geometrische Figur ist das Dreieck:
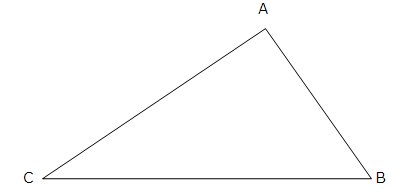
Der Umfang des Dreiecks ergibt sich durch
wobei 
die Länge des Segments AB ist, und so weiter.
Wenn ein Dreieck zwei gleich lange Seiten hat, so wird es gleichschenkelig genannt, und wenn alle Seiten gleich lang sind, so handelt es sich um ein gleichseitiges Dreieck.
Eine weitere sehr gebräuchliche geometrische Figur ist das Quadrat; ein Rechteck mit vier gleich langen Seiten (Kantenlänge) 
.
Sein Umfang ist 
.
Nun, sehen wir uns diese beiden Dreiecke an:
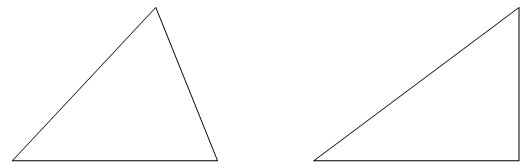
Wir sehen, dass die beiden Seiten der Dreiecke unterschiedliche Neigungen haben. Ein genauer Blick auf die rechten Seiten der Dreiecke macht dies verständlicher:
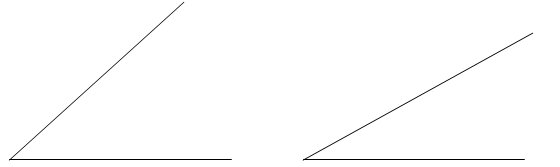
Der Unterschied zwischen den beiden Segmenten (links weiter geöffnet als rechts), wird der Winkel zwischen den Segmenten genannt. Der größte mögliche Wert ergibt sich, wenn ein Segment das andere nach rechts oder links verlängert, also eine längere Gerade bildet. Der kleinstmögliche Wert wäre, wenn zwei Segmente aufeinander zu liegen kommen.
Winkel werden in Grad gemessen. Ihr Wert reicht vom Minimum 0 bis zum Maximum von 180. Den Mittelwert von 90 erhalten wir, wenn sich das obere Segment in vertikaler und das untere Segment in horizontaler Position befindet:
Den gleichen Winkel erzielen wir, wenn wir ein Senkblei an einer Schur an eine horizontale Fläche halten.
Winkel werden mit dem Winkelmesser gemessen:
Alle Winkel eines Rechtecks betragen 90 Grad. Ein Winkel von 90 Grad wird auch „rechter Winkel“ genannt.
Kommen wir nochmals zurück auf das rechteckige Stück Land von zuvor. Wenn wir nun wissen wollen, wie groß es ist, so müssen wir dessen Fläche berechnen. Erinnern wir uns daran, dass die gegenüberliegenden Seiten eines Rechtecks gleich lang sind. Wir bezeichneten die lange Seite mit 
und die kurze mit 
. Die Fläche daraus errechnet sich wie folgt:
Für ein Quadrat ist die Fläche
Für ein Dreieck, bei welchem ein Winkel 90 Grad beträgt, können wir dessen Fläche auf der Basis eines Rechtecks berechnen: Wir verdoppeln das Dreieck, bilden aus den zwei Dreiecken ein Rechteck und sehen gleich, dass die Fläche dieses Dreiecks die Hälfte der Rechtecksfläche beträgt:
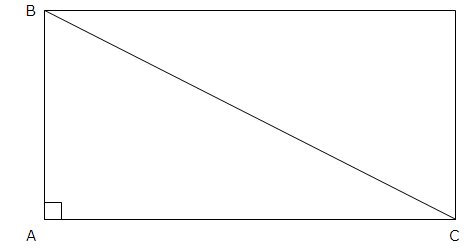
Für ein beliebiges Dreieck ist die Flächenberechnung aufwendiger:
Als letzte geometrische Figur, wollen wir nun den Kreis diskutieren:
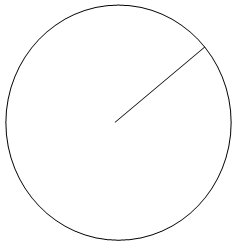
Münzen, CDs, Linsen, etc., sie alle haben Kreisform. Ein Kreis ist dadurch definiert, dass jeder Punkt auf ihm gleich weit vom Mittelpunkt des Kreises entfernt ist. Dieser fixe Abstand wird Radius 
genannt.
Der Kreisumfang ist die Länge der durch den Radius festgelegten Kreislinie, von einem beliebigen Punkt des Kreises aus gemessen bis an diesen Punkt. Die Formel zur Berechnung des Kreisumfangs ist:
Die Zahl 
ist eine reelle Zahl mit einer unendlichen Anzahl von Dezimalen, davon verwenden wir hier nur zwei Dezimalstellen:3.14 Der Umfang eines Kreises mit Radius 20 ist daher ungefähr 125,6.
Die Kreisfläche wird durch folgende Formel beschrieben:
Bei dem selben Kreis wie oben angenommen mit , beträgt die Kreisfläche damit
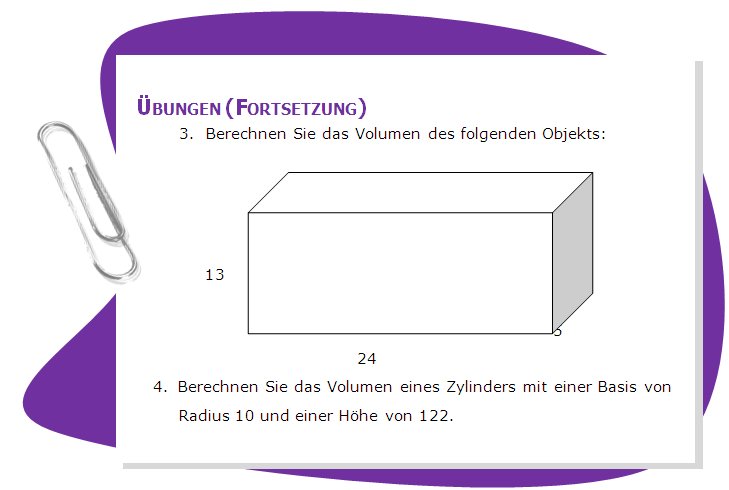
Im realen Leben haben wir es nicht nur mit den bisher besprochenen geometrischen Figuren zu tun. So ist z.B. ein Ziegelstein nicht nur ein Rechteck, sondern er hat eine dritte Dimension, welche in zu einem (dreidimensionalen) Körper macht:
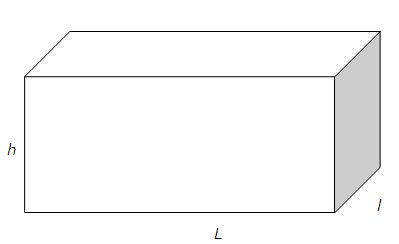
Diese Form nennt sich Quader. Alle Seiten eines Quaders sind Rechtecke. Ein Quader hat 3 Dimensionen im Gegensatz zum Rechteck, welches nur 2 Dimensionen hat. Die Dritte Dimension bezeichnen wir als Höhe h.
Wir können die Oberfläche des Quaders berechnen, wenn wir die ihn umgebenden Flächen aufsummieren. Am Wichtigsten ist es, sein Volumen berechnen zu können. Das Volumen lässt sich auch als die Wassermenge denken, die man in das Objekt einfüllen könnte, wenn es eine nach oben offene Box wäre.
Die Formel zur Berechnung des Volumens eines Quaders ist
Für einen gleichseitigen Quader, auch Würfel genannt, ist das Volumen
wobei die Länge einer beliebigen Seite des Würfels ist.
Eine andere dreidimensionale Form, die wir überall in der Natur finden können, ist der Zylinder:
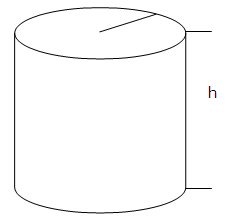
Ein Eimer ist ein Zylinder und ein Wasserglas kann ein Zylinder sein. Der Zylinder hat einen Kreis als Basis, mit einen Radius 
, und einer Höhe 
. Das Volumen des Zylinders ergibt sich durch:
Das Volumen eines Eimers von 30cm Höhe und einem Radius von 15cm ist damit
