Key Competencies Kit
for Facing Lifelong Learning


 |
Този проект е финансиран с помощта на Европейската комисия. Този документ отразява гледната точка единствено на автора и Комисията не може да бъде отговорна за употребата на информацията в него. |
 |
След приключването на този дял Вие ще можете да:
В природата може да намерите много видове предмети, с различни форми. Тези форми се наричат геометрични фигури.
Най-простият геометрична фигура е отсечката. Можем да я изобразим като легнала струна. .
Ето и изображение на отсечката:
Най-важната характеристика на един отсечка е дължината му. Всяко разстояние между два обекта може да се мисли като отсечка - по-къса или по-дълга и затова ние трябва да намерим начин за измерване на тази дължина. За да се направи, че ние ще използваме линийка, която представлява например летвичка с еднакви по дистанция единици отбелязани върху нея.

Когато имаме повече от две отсечки се касае за геометрична фигура.
Най-популярна сред тях е правоъгълника, който има четири прави ъгъла във всеки край. Обозначаваме ги с А, В, С и D. :

В реалния живот предмети с такава форма са вестник, лист хартия, обикновено стените, тухла и тн.
Да приемем, че това е една къща парцел, и ние трябва да се направи ограда за него. Ние трябва да знаем колко дървени талпи са необходими, за да се направи ограда.
За да разберем колко е цялата дължина ние трябва да намерим така наречения периметър на парцела (правоъгълник).
Страните на правоъгълника са AB, BC, CD и AD, така че периметъра (обозначен с буквата “P”) е равен на:
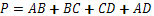
Важно е да знаем, че за един правоъгълник срещуположните страни са равни. Ще означим с ![]() дължината на дългите страни, а с
дължината на дългите страни, а с ![]() дължината на късите страни. По този начин периметъра е равен на:
дължината на късите страни. По този начин периметъра е равен на:

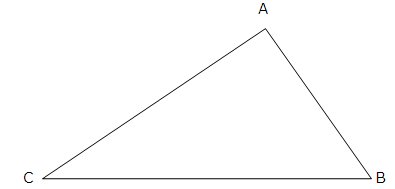
Параметърът на триъгълника е както следва:
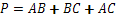
където ![]() е дължината на отсечка AB и т.н.
е дължината на отсечка AB и т.н.
Ако триъгълника има две равни страни, то той се нарича равнобедрен, а когато всички страни са равни се нарича равностранен.

Периметърът е  .
.
Нека сега да поговорим за ъглите в триъгълниците:
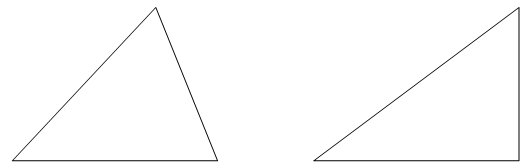
Ще забележим, че страните на триъгълниците имат различно разположение и големина на ъглите. Този в дясно има сключен прав ъгъл в дясната му долна част.
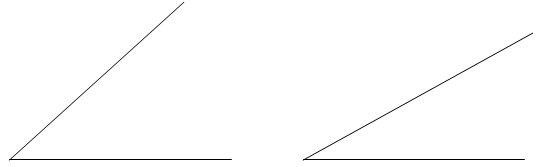
На горната картинка пък са изобразени два ъгъла, от които левия е по-голям. Максималната големина на един ъгъл е 360 градуса. Ъгъл, които е по-малък от 90 градуса се нарича остър. Ъгъл, който е точно 90 градуса се нарича прав, а които е по голям от 90 градуса – тъп. В зависимост от вида ъгли различаваме: правоъгълник (с един прав ъгъл), остроъгълен триъгълник (с поне два остри ъгли) и тъпоъгълен триъгълник (с поне един тъп ъгъл).
Ъглите могат да бъдат измервани и с помощта на ъгломер, които можете да видите на следващата картинка.


В средата на ъгломера се намират правата линия за прав ъгъл от 90 градуса. В ляво от него са тъпи ъгли, а в дясно остри.
Нека се върнем към правоъгълната фигура и да се опитаме да намерим каква е повърхнината (площта). Припомняме Ви, че срещуположните страни на правоъгълника са равни и съответно ги отбелязваме с ![]() и
и ![]() . И така повърхнината е:
. И така повърхнината е:
(не забравяйте, че знака “–“ се използва вместо “х”)
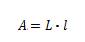
При куб, повърхнината е равна на:
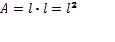
За триъгълник, които има прав ъгъл на 90 градуса може да пресметнем като удвоим триъгълника и го поставим над другия триъгълник и така те ще образуват правоъгълник. Тогава повърхнината може да бъде пресметната по следния начин:
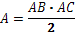
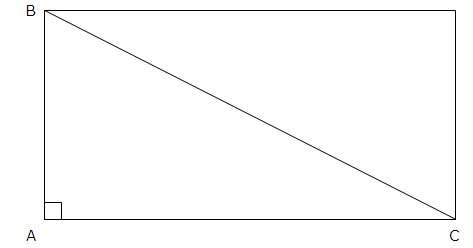
За обикновен триъгълник повърхнината се намира малко по-сложно както следва:

Последната фигура, която ще Ви представим е кръг:
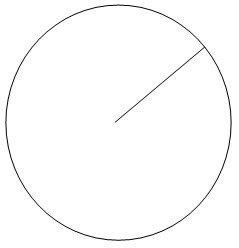
Има много предмети, които могат да бъдат описани като кръг – монети, компакт дискове, лещи и др. При кръга всяка точка по окръжността му се намира на равно отстояние от центъра му. Тази отсечка се нарича радиус и се отбелязва със знак “ ![]() ”.
”.
За да намерим обиколката (окръжността) на кръг трябва да направим следното:
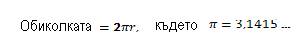
Числото “пи” ![]() е реално число, обикновено се записва до втория знак след десетичната точка, а именно
е реално число, обикновено се записва до втория знак след десетичната точка, а именно ![]() .
.
И така обиколката на кръг с радиус 20 е около 125,6.
Повърхнината на кръг се намира по следната формула:
![]()
Ако радиуса е  , то тогава повърхнината ще бъде:
, то тогава повърхнината ще бъде:
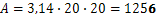
В реалния живот откриваме и други фигури, подобни или видоизменени на посочените по горе. Кубът е не просто правоъгълник, тъй както се вижда на фигурата по долу, той има друго измерение:

Тази сянка се нарича паралелепипед и всяка негова страна представлява правоъгълник. Това е триизмерно тяло, което за разлика от правоъгълника има трето измерение.
То се отбелязва със знака “ h “ и отбелязва височината на куба. Най-важното при куб е да намерим неговия обем. За да пресметнем обем може да си представим обема на вода, които има височина h, дължина L и ширина l
Формулата за намиране на обем е:
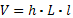
За паралелепипед с равни страни, го наричаме куб. За да намерим неговия обем:
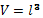
където ![]() е отбелязва дължината.
е отбелязва дължината.
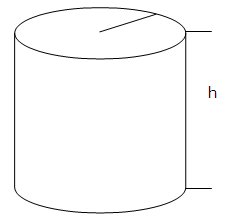
Чашата вода представлява цилиндър. Той е построен на основата на кръг с радиус, отбелязван с ![]() , и височина
, и височина ![]() . Обемът може да бъде намерен по следния начин::
. Обемът може да бъде намерен по следния начин::

Например обемът на цилиндър с височина 30 cm и радиус 15 cm е
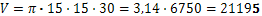
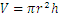
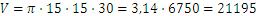

 |
Отговори |