Geometrija

 

	This Project has been funded with support from the European Commission.  This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein.

 

TIKSLAI

Perskaitę šį skyrių sugebėsite:

• Atpažinti pagrindines geometrijos figūras ir formas: linijas, trikampius, stačiakampius
• Apskaičiuoti ilgį, atstumą ir kampus
• Apskaičiuoti paviršiaus plotą ir tūrį

 

ĮVADAS. GEOMETRINĖS FIGŪROS. ILGIS

Gamtoje galime sutikti įvairių daiktų su skirtingomis formomis. Tos formos yra vadinamos geometrinėmis figūromis.
Paprasčiausia geometrinė figūra yra atkarpa. Ją galime pavaizduoti kaip liniją su užbaigtais kraštais.
Atkarpa:
 

Svarbiausia atkarpos savybė yra jos ilgis. Kiekvienas atstumas tarp dviejų objektų gali būti tam tikra ilgesnė ar trumpesnė atkarpa, tad mes turime žinoti kaip apskaičiuoti tos atkarpos ilgį. Tam galime panaudoti liniuotę, kurioje yra sužymėti ilgio vienetai.

Kitos geometrinės figūros turi daugiau nei vieną atkarpą. Viena iš svarbiausių figūrų yra stačiakampis:

 

Mūsų gyvenime aplinkui pilna stačiakampių – pavyzdžiui, laikraštis, popieriaus lapas, dirbamas žemės laukas, siena ir t.t. 
Tarkime, kad tai yra namų plotas ir mums jį reikia aptverti tvora. Norime sužinoti kiek reikės medinių lentų tai tvorai pagaminti.
Matmuo, kuris nusako visą tos tvoros ilgį vadinamas stačiakampio perimetru ir yra gaunamas sudėjus visas jo šonines atkarpas.
Pažymėkime tas atkarpas AB, BC, CD ir AD, perimetras yra
Svarbu pastebėti, kad stačiakampio priešingos kraštinės yra lygios, taigi ilgesnes kraštines pažymime  , o trumpesnes . Perimetro formulė atrodo taip

Kita paprasta geometrinė figūra yra trikampis :

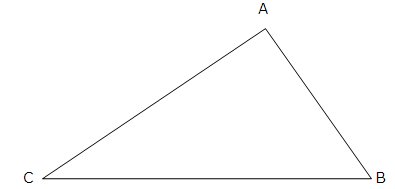
Trikampio perimetras apskaičiuojamas taip

yra kraštinės AB ilgis ir t.t.
Jeigu trikampis turi dvi vienodas kraštines, jis yra vadinamas lygiašoniu, o jeigu visos kraštinės vienodos tuomet jis vadinamas lygiakraščiu trikampiu.
Kita labai dažnai sutinkama geometrinė figūra – kvadratas, tai stačiakampis kurio visos kraštinės yra lygios, pažymime jas .

Kvadrato perimetras yra .

KAMPAI

Pažvelkime į šiuos du trikampius:

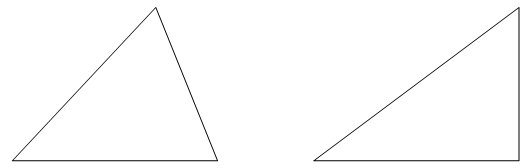
Pastebime, kad abiejų trikampių kraštinės yra skirtingai palinkusios. Pažvelkime atidžiau tik į kairines kraštines:

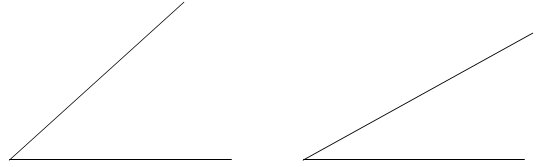
Atstumas tarp dviejų atkarpų yra vadinamas kampu, jis mažesnis dešinėje pusėje, o kairėje didesnis. Didžiausias kampas tarp atkarpų yra kai viena atkarpa į dešinę tolygiai pratęsia kitą atkarpą į kairę, o mažiausias kai atkarpos yra viena ant kitos. 
Kampai yra matuojami laipsniais ir svyruoja nuo 0 iki 180. 90-ies laipsnių kampą sudaro dvi atkarpos, kai viena yra bertikalioje pozicijoje, o kita horizontalioje:

Toks pat kampas būtų gaunamas, tarp vertikaliai pakabintos virvės ir horizontalaus paviršiaus
Kampai yra matuojami su matlankiu:

Visi stačiakampio kampai yra po 90 laipsnių. Kampas kuris sudaro 90 laipsnių yra statusis kampas.

PLOTAS

Grįžkime prie stačiakampio formos žemės sklypo, tarkime, kad norime apskaičiuoti kiek ten yra žemės. Matmuo, kuris parodo stačiakampio paviršių vadinamas plotu. Prisiminkime, kad stačiakampio priešingos kraštinės yra lygios ir žymimos  bei . Taigi plotas yra

Kvadrato plotas yra

Stačiakampio trikampio, kurio vienas kampas yra 90 laipsnių, plotas apskaičiuojamas remiantis pačiu stačiakampiu: trikampį nukopijuojame ir pavaizduojame virš pirmojo, taip kad abu sudarytų stačiakampį, kaip pavaizduota žemiau esančiame paveikslėlyje. Tuomet trikampio plotas bus lygus pusei stačiakampio ploto. 

                   

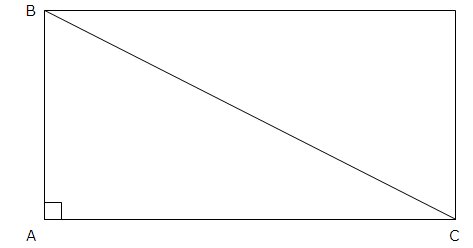
Paprasto trikampio plotą apskaičiuoti yra kiek sunkiau:

Paskutinė geometrijos figūra, kurią aptarsime yra apskritimas:

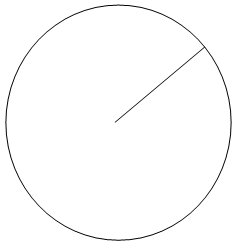
Yra daugybė apskritimo formos daiktų, pavyzdžiui: monetos, kompaktiniai diskai ir t.t. Apskritimo viena iš savybių yra, kad nuo centrinio taško kiekviena kraštinės vieta yra vienodai nutolusi. Šis atstumas yra vadinamas spinduliu .
Apskritimo perimetras yra kraštinės ilgis aplink jį. Jis apskaičiuojamas tokia formule:

Skaičius  yra realusis skaičius su begaline liekana, dažniausiai užrašomas suapvalintas: .
Taigi, jeigu apskritimo spindulys lygus 20, tai perimetras bus apytiksliai 125,6.
Apskritimo plotas apskaičiuojamas pagal tokią formulę:

To paties apskritimo, kurio spindulys ,plotas yra

TŪRIS

Kasdien susiduriame ir su kitokiomis figūromis, kurių dar nepaminėjome. Pavyzdžiui, plyta yra ne tik stačiakampio formos:
             

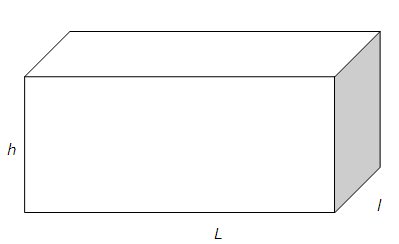
Tokia figūra yra vadinama gretasieniu, o jo visos sienos yra stačiakampiai. Tai yra trimatis kūnas, tad jis turi dar vieną matmenį.
Trečiasis matmuo žymimas h ir vadinamas aukščiu.
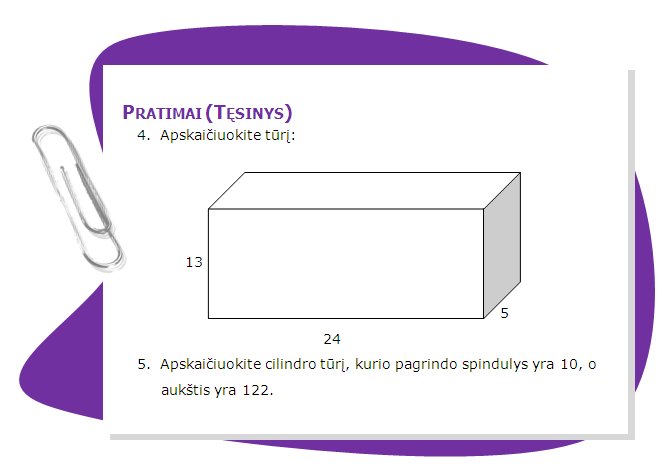
Mes galime apskaičiuoti figūros paviršiaus plotą, jei sudėsime visų stačiakampių plotus, bet svarbiausias matas yra tūris. Tūrį galėtume apibūdinti kaip vandens kiekį, kuris tilptų į dėžę, turinčia h aukštį, L ilgį ir l plotį. Tūrio formulė yra tokia:

Gretasienis, kurio visos kraštinės yra lygios vadinamas kubu, jo tūris yra:

  yra kraštinės ilgis.

Kita trimatė figūra yra cilindras:

                                                               

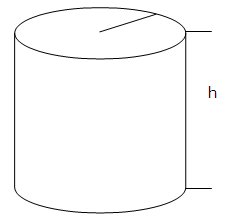
Kibiras yra cilindro formos, taip pat kaip ir stiklinė. Cilindras turi apskritimą, kaip pagrindą, turi spindulį , ir aukštį . Tūris apskaičiuojamas taip:

Pavyzdžiui, kibirėlio tūris, kurio aukštis 30 cm ir spindulys 15 cm yra