Key Competencies Kit
for Facing Lifelong Learning


 |
This Project has been funded with support from the European Commission. This communication reflects the views only of the author, and the Commission can not be held responsible for any use which may be made of the information contained therein. |
 |
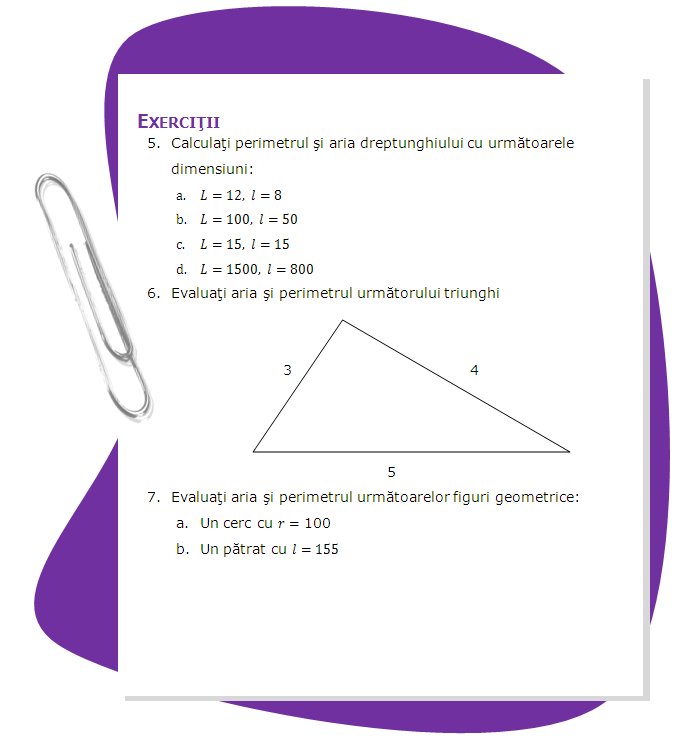
La finalizarea acestei unităţi veţi fi capabil să:
În natură întâlnim diverse tipuri de obiecte, de diferite forme. Aceste forme se numesc figuri geometrice.
Cea mai simplă figură geometrică este segmentul. Putem să ne imaginăm uşor un segment ca o bucată de sfoară, fixată la ambele capete.
Un segment:
Cea mai importantă caracteristcă a unui segment este lungimea sa. Din vreme ce orice distanţă intre două obiecte poate fi considerată un segment, mai scurt sau mai lung, avem nevoie de o metodă de a măsura această lungime. Pentru aceasta, vom folosi o riglă, adică o bucată dreaptă de lemn, marcată cu unităţi situate la distanţe egale.

Următorul pas în definirea figurilor geometrice este de a avea mai mult decât un segment. Una dintre cele mai importante figuri geometrice este dreptunghiul:

Există multe dreptunghiuri în viaţa reală – de exemplu un ziar, o bucată de hârtie, un câmp agricol, un zid, şi aşa mai departe.
Să presupunem că avem o parcelă de pământ şi vrem să o ingrădim. Trebuie să ştim de câte scânduri de lemn avem nevoie pentru a face gardul.
Mărimea care ne furnizează lungimea totală a gardului poartă numele de perimetrul parcelei (dreptunghiului) şi este egală cu suma laturilor sale.
Presupunând că laturile sunt AB, BC, CD şi AD, perimetrul est
![]()
O observaţie importantă este că, pentru un dreptunghi, laturile opuse sunt egale, astfel vom nota cu lungimea celei mai lungi şi cu l lungimea celei mai scurte. Astfel, perimetrul este dat de
![]()
Există şi alte tipuri de figuri geometrice care ne interesează, cea mai simplă fiind triunghiul:
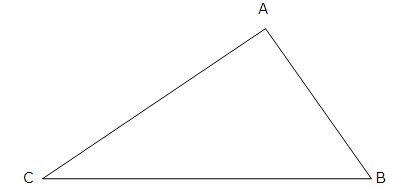
Perimetrul triunghiului este dat de
![]()
este lungimea segmentului AB, şi aşa mai departe.
Dacă un triunghi are două laturi egale, atunci se numeşte isoscel, iar dacă toate laturile sunt egale, se numeşte echilateral.

O altă figură geometrică des întâlnită este pătratul, care este un dreptunghi cu toate laturile egale, notate cu ![]() .
.
Acum, să privim aceste două triunghiuri:
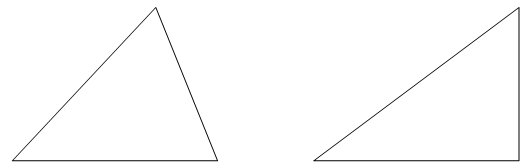
Putem observa că laturile au înclinări diferite în cele două triunghiuri. Dacă privim mai atent doar laturile din stânga triunghiurilor, vom înţelege mai bine:
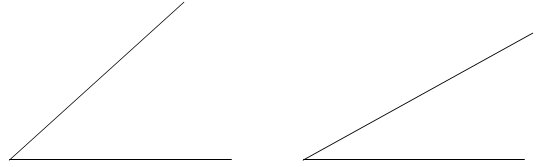
Diferenţa între cele două segmente, care este mai mică în partea dreaptă şi mai mare în partea stângă, se numeşte unghiul dintre cele două segmente. Valoarea maximă posibilă se obţine când două segmente sunt unul în continuarea celuilalt, unul la stânga, celălalt la dreapta. Valoarea minimă se obţine când segmentele sunt unul peste altul.
Unghiurile se măsoară în grade, de la un minim de 0 grade până la un maxim de 180. Valoarea de mijloc, 90 grade, se obţine când segmentul de sus este în poziţie verticală, iar cel de jos este în poziţie orizontală:

Se obţine acelaşi unghi dacă atârnăm o sfoară cu plumb la un capăt peste o suprafaţă orizontală.
Unghiurile se măsoară cu următorul instrument:

Toate unghiurile unui dreptunghi au 90 grade. Un unghi de 90 de grade se numeşte un unghi drept.
Să ne întoarcem la parcela dreptunghiulară de pământ şi să presupunem că vrem să ştim cât pământ cuprinde. Mărimea care ne dă răspunsul la întrebare este aria, sau suprafaţa dreptunghiului. Să ne amintim că laturile opuse ale dreptunghiului sunt egale şi sunt notate cu. Atunci aria este
![]()
Pentru un pătrat, aria este
![]()
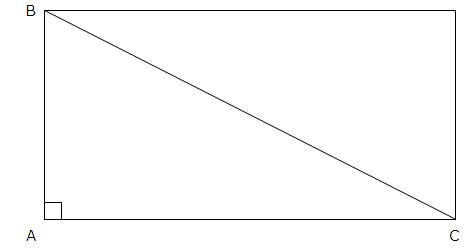
Pentru un triunghi care are un unghi de 90 de grade, adică are un unghi drept, putem calcula aria bazându-ne pe aria unui dreptunghi, în modul următor: dublăm triunghiul, plasăm cel de-al doilea triunghi deasupra primului, astfel încât formează împreună un dreptunghi, ca în figura de mai jos. Atunci aria triunghiului va fi jumătate din aria dreptunghiului, adică
![]()
Pentru un triunghi oarecare, aria se calculează mai complicat:
![]()
Ultima figură geometrică importantă pe care o vom discuta este cercul:
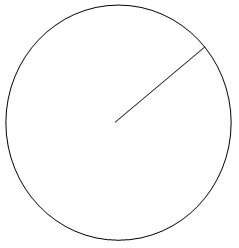
Există multe obiecte care pot fi descrise de cercuri, cum ar fi monedele, CD-urile, lentilele, etc. Cercul poate fi descris de faptul că orice punct al său se află la o distanţă egală de un punct fix numit centru. Această distanţă fixă se numeşte raza r.
Circumferinţa cercului sau perimetrul este lungimea totală măsurată de-alungul cercului. Formula pentru calculul circumferinţei este următoarea:
![]()
Numărul este un număr real, cu un număr infinit de zecimale, aproximat de regulă la .
Astfel, circumferinţa unui cerc cu raza de 20 este aproximativ 125,6.
Aria cercului este dată de următoarea formulă:
![]()
Adică pentru cercul de mai sus, cu , aria este
![]()
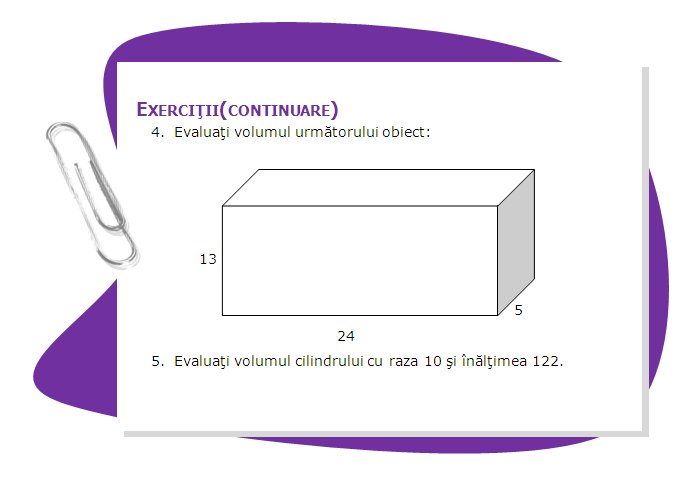
În viaţa reală întâlnim şi alte tipuri de obiecte, nu numai figurile menţionate până acum. De exemplu, o cărămidă nu este doar un dreptunghi, deoarece mai are o dimensiune care o defineşte:
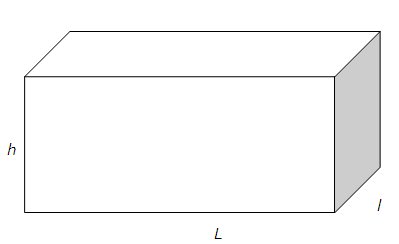
Figura se numeşte paralelipiped şi toaţe feţele sale sunt dreptunghiuri. Acesta este un corp tridimensional, adică are trei dimensiuni diferite, în comparaţie cu dreptunghiul, care are doar 2.
Cea de-a treia dimensiune este notată cu h şi se numeşte înălţimea obiectului.
Putem calcula suprafaţa obiectului dacă adunăm toate suprafeţele sale, dar cea mai importantă mărime este volumul.
![]()
Pentru un paralelipiped cu toate laturile egale, numit şi cub, volumul este
![]()
este lungimea laturii
Un alt tip de formă tridimensională pe care o putem întâlni în natură este cilindrul:
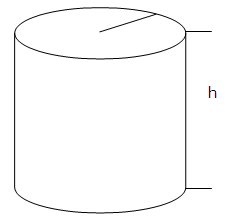
O găleată este un cilindru şi un pahar de sticlă este de asemenea un cilindru. Cilindrul are baza formată dintr-un triunghi, o rază şi o înălţime . Volumul este dat de:
![]()
De exemplu, volumul unei găleţi cu înălţimea de 30 cm şi raza bazei de 15 cm este
![]()