Цели числа: Числови системи и геометрични изчисления

 

	Този проект е финансиран с помощта на Европейската комисия. Този документ отразява гледната точка единствено на автора и Комисията не може да бъде отговорна за употребата на информацията в него.

 

Цели

След успешно приключване на модула обучаемият ще може да:

• Разбирате използването на целите числа
• Разбирате концепцията на отрицателните числа
• Разбирате и изпълнявате основните операции с физически и цели числа

 

Въведение и основни операции

Естествените числа са възникнали в думите, използвани за брой неща, започвайки с номер 1. Много по-късно се е развила идеята за нула като число със собствената си цифра.

Поредицата от цели числа се обозначават със знак 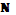 и съдържат следните числа както следва:

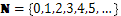
Основните операции могат да бъдат извършвани като добавим знака “+” към всяко естествено число, без числото 0.
Ето няколко примера:

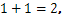
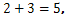
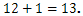
Добавянето на две числа е практически преброяването заедно на две групи. Правилата за допълнение се основават на допълнения между първите 10 естествени числа, известен също като цифри:

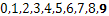
Всяко добавяне към тези числа се основава на операция между тези 10 цифри.

1	8	+
2	3
1+2+1=4	8+3=11
4	1

Втората основна операция от естествени числа е логаритмична, което е обратното на допълнение. За естествени числа, броят на взетите числа винаги трябва да бъде по-малък или равен от първоначалния.
Моля, вижте примера:

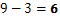
Както се вижда ако към получения резултат добавим отново числото при изваждане, то получаваме отново същото число, от което сме извадили.

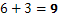
Ако искаме да извършваме смятане с цифри, които не са цели числа, то отново може да използваме правилото за допълнение. Този път, вместо да “транспортираме” на цифрата от ляво, то изваждаме същата цифра, която е по-малка от тази, от която изваждаме. Вижте следния пример:

5	3	-
2	1
5-2=3	3-1=2
3	2

 

5	1	-
2	8
(5-1)-2=2	11-8=3
2	3

Във скобите поставяме ново изваждане, което ни дава краен резултат, от които да направим допълнителното изваждане 4-2=2.
Следва да направим следното: вместо да събираме еднакви цели числа, ние бихме могли да умножим техния брой по техния номинал и така да получим по бързо крайния резултат. Операцията се нарича “умножение”.

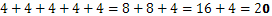
Но по лесно е да умножим:

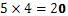
с други думи казано имаме “пет пъти цифрата четири”, което прави сбор 20.
Когато се умножи броя с повече от една цифра, се прилагат същите правила както следва: само последната цифра е написана, а останалата част се "транспортира" от ляво и се добавя към резултата от умножението. Всяка от цифрите, се умножава с цифрите по-долу, като се започне от ляво на дясно. Ето един пример, когато второто число е само на цифри:

1	3	×
	7
1×7+2=9	3×7=21
9	1

Ако второто число е двуцифрено, същите операции се повтарят, и резултатът е изместен с една позиция в ляво, както в примера по-долу:

	1	3	×
	2	7
	1×7+2=9	3×7=21
1×2=2	3×2=6
2+1=3	9+6=15	1

Трябва да се отбележи, че всеки умножаване от 0 е 0.
Пълната таблица за умножение на числата от 1 до 10 е посочена по-долу:

Противоположната операция на умножението се нарича делене. Обозначава се със знак “÷” или “:”. Следващия пример ясно показва тази обратна зависимост:

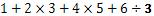
Ако 3×5=15, то тогава 15:5=3.
Тоест ако умножаваме по цифрата 5 то и делението ни на нея от предишния сбор ще бъде същия, от които сме започнали със операцията умножение.

Поредица от операции

Ако искаме да извършим операция в поредица от действия, които включват например събиране, умножение и делене както на пример:

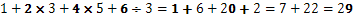
ние трябва да изготвим поредица от действия, за да можем да получим крайната сума. Първо трябва да извършим процесите на умножение и делене на целите числа и след това да извършим процедурата по събиране.

Може да си помагаме и като поставим в скоби по малките операции от събиране и изваждане и първо да си помогнем като решим тях, а едва след това можем да продължим в тяхното умножение и делене.

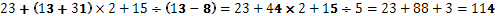
Скобите могат да бъдат приложение и в следващия пример:

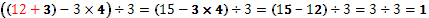
Има няколко прости правила, които се прилагат при използването на скобите. Например числото, от което ще стартираме ще го умножаваме по-отделно със всяко число от посоченото в скобите и така ще получим крайната сума.

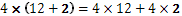
Генералното правило гласи, че когато   са цели числа може да извършваме следните помощни операции:

 

Представяне на естествените числа

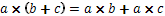
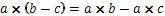
В следващата поредица показваме по какъв начин се подреждат естествените числа в права линия.

0    1    2    3    4    5    6    7                           a     a+1

Първо представяме числото 0, след което в хоризонталната линия представяме поредица от естествени числа получени като към всяко следващо сме добавили цифрата 1. Така увеличението с цифра 1 може да продължи до безкрайност. По същия начин можем да направим и обратната редица, само че с отрицателен знак “-“.  
Винаги номера, които се намира в дясно от началния е по-голям от изначалния.
Например числото 5 е по-голямо от числото 3, така, че ние бихме могли да използваме знака наречен “по-голям” изобразен като “>”

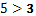
По същия начин можем да използваме знака наречен “по-малко”, който ще бъде изобразен “<”. Ето един пример:

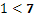
Забележете, че когато се извади, първото число трябва винаги да бъде по-голямо от второто. Ако добавите означава, че преминавате към следващата позиция на дясно по хоризонталната ос, а след това ако изваждате то тогава числата ще се разполагат наляво по същата ос. Ако се движим наляво с няколко единици по-малко от сегашната позиция ние ще получаваме друго естествено число, което е в резултат на изваждане на резултата.
Ето как ще изглежда и поредицата по хоризонталната ос, ако имаме комбинация от числа, получени при събиране и такива, получени при изваждане. И в двете посоки сумата може да се увеличава или намалява до безкрайност.

  

                                  -4   -3   -2   -1    0    1    2   3

Ако следваме основните операции например на изваждане ще получим следния пример:

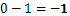
По същия принцип може да направим и следните примери:

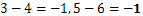
Можем също така да определим изваждането между всеки две естествени числа като изваждане между по-големите и по-малък брой. Например:

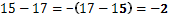
Както се вижда 17 е по-голямо от 15 и затова има знак минус пред него.
Ето още няколко примера за действия на естествените числа:

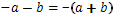
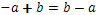
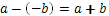
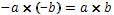
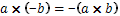
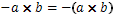
Обърнете внимание,че:

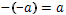
за всяко естествено число на мястото на “a”.